Introduction to Rainbow Coloring of Graphs
In graph theory, rainbow coloring of graphs is an edge coloring technique of the graphs.
An edge coloring of a graph is a function from its edge
set to the set of natural numbers.
A path in an edge colored graph with no two edges sharing the
same color is called a rainbow path.
An edge colored graph is said to be rainbow connected if every pair of vertices is connected by at least one rainbow path. Such a
coloring is called a rainbow coloring of the graph G.
If a rainbow coloring uses k colors, we call it a k-rainbow coloring.
Let c be a rainbow coloring of a connected graph G. For two vertices u and v of G, a rainbow
u−v geodesic in G is a rainbow u−v path of length d(u, v), where d(u, v) is the distance between u and v (the length of a shortest u−v path in G).
The graph G is strongly rainbow-connected if G contains a rainbow u−v geodesic for every two
vertices u and v of G. In this case, the coloring c is called a strong rainbow coloring of G.
Let c be a rainbow coloring of a connected graph G. For two vertices u and v of G, a rainbow
u−v geodesic in G is a rainbow u−v path of length d(u, v), where d(u, v) is the distance between u and v (the length of a shortest u−v path in G).
The graph G is strongly rainbow-connected if G contains a rainbow u−v geodesic for every two
vertices u and v of G. In this case, the coloring c is called a strong rainbow coloring of G.
History
The concept of rainbow coloring of graphs has been introduced by Chatrand et.al (ref 1).
Definitions and Bounds
- Rainbow connection number of a graph G , denoted by rc(G) is the minimum number of colors required to rainbow color a connected graph.
- A rainbow coloring using rc(G) colors is called a minimum rainbow coloring.
- The strong rainbow connection number of a graph G is the minimum number of colors needed to strong rainbow color G, and is denoted by src(G).
- A strong rainbow coloring of G using src(G) colors is called a minimum strong rainbow coloring of G.
In order to rainbow color any connected graph G,we can see that at least diam(G) colors are required, where diam(G) is the diameter of G (i.e.
the length of the longest shortest path).
On the other hand, we can never use
more than m colors, where m denotes the number of in G. Finally, because each strong rainbow colored graph
is rainbow colored, we have
diam(G ) ≤ rc(G) ≤ src(G) ≤ m.
Rainbow Coloring and Strong Rainbow Coloring of Petersen Graph
Rainbow Coloring of Petersen Graph
Consider the Petersen graph P given below. It shows a rainbow 3-coloring of P. Thus rc(P)≤ 3. On the other hand, if u and v are two nonadjacent vertices of P, then d(u, v) = 2. So the length of a u − v path is at least 2.
Thus any rainbow coloring of P uses at least two colors and so rc(P) > 2. If P has a rainbow
2-coloring c, then there exist two adjacent edges of G that are colored the same by c, say e = uv and
f = vw are colored the same. Since there is exactly one u − w path of length 2 in P, there is no rainbow u − w path in P, which is a contradiction.
Therefore, rc(P) = 3.
Strong Rainbow Coloring of Petersen Graph
Since rc(P) = 3, it follows that src(P) ≥ 3. It is known that the edge chromatic number of the Petersen graph is known to be 4. So, any 3-coloring c of the edges of P results in two adjacent edges uv and vw being assigned the same color. Since u, v,w is the only u − w geodesic in P, the coloring c is not a strong rainbow coloring. Since the 4-coloring of the edges of P in the figure below is a strong rainbow coloring, hence src(P) = 4.
 |
| Strong Rainbow Coloring of Petersen Graph |
The following are the extremal
cases:
The following are the extremal cases:
- rc(G) = src(G) = 1 if and only if G is a complete graph.
- rc(G) = src(G) = m if and only if G is a tree.
Rainbow Coloring and Strong Rainbow Coloring of Cycle Cn
Consider a cycle on n vertices, Cn. We know that the
diam(Cn) = ⌊n/2⌋. Hence, src(Cn) ≥
rc(Cn) ≥
⌊n/2⌋. This lower bound
for rc(Cn) and src(Cn) is
nearly the exact value of these numbers. Thus, this leads to the following
proposition:
For each integer n ≥ 4,
rc(Cn) = src(Cn) = ⌈n/2⌉.
Rainbow Coloring and Strong Rainbow Coloring of Wheel Wn
Consider a wheel graph on n vertices Wn.
For n ≥ 3, the rainbow connection number of the wheel Wn is
For n ≥ 3, the rainbow connection number of the wheel Wn is
rc(Wn) = 1 if n=3
=2 if 4 ≤ n ≤ 6
=3 if n ≥ 7.
For n
≥ 3, the strong rainbow
connection number of the wheel Wn is
src(Wn) =
⌈n/3⌉.
Rainbow Coloring of Cube
Consider a d dimensional cube Qd .
- If d ≥ 4, d ≠ 5, then rc(Qd) = d.
- If d ≥ 3, d ≠ 4, there exists a total (d + 1)-coloring of Qd , which is also a rainbow coloring.
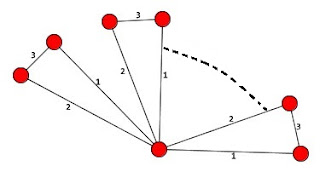
Rainbow Coloring of Fan Graph
A Fan graph Fn is a graph
obtained by joining n copies of the cycle graph C3 with a common vertex. Fn is a planar undirected graph and has 2n+1 vertices and 3n edges.
Rainbow Coloring of Flower Graph
A Flower graph is
obtained from a helm graph by
joining each pendant vertex of the helm graph
to the central vertex of the helm graph.
The Helm graph Hn is the graph
obtained from a wheel graph by
attaching a pendant edge at each vertex of the n-cycle.
If (n-1) petal edges are attached
at the central vertex of wheel graph Wn for n≥4 , then the rainbow coloring of the
resulting graph G is rc(G)=3.
Rainbow Coloring of Corona
The corona graph G, Pn o K2 has a rainbow coloring rc(G)=2n-1, where n is the number of vertices in the path.
The corona graph G, Pn o C4 has a
rainbow coloring rc(G)=n+1, where n is the number of vertices in the
path.
 |
| Rainbow Coloring of P3 oK2 |
 |
| Rainbow Coloring of PnoK2 |
Rainbow Coloring and Strong Rainbow Coloring of a Complete Bipartite Graph
For integers s and t with 2 ≤ s ≤ t,
Strong Rainbow Coloring of a Complete Multipartite Graph
Consider a complete multipartite graph
where k ≥ 3, and n1 ≤ n2 ≤….≤ nk
such that
and
Then,
Complete and Incomplete Rainbow Coloring
Consider a connected graph G with a k-rainbow coloring.
- If a rainbow path in G has length k, then such a path is known as a complete rainbow path. Else, it is known as an incomplete rainbow path.
- A rainbow coloring of G is incomplete if for any vertex u in V (G), G has at most one vertex v such that all the rainbow paths between u and v are complete.Otherwise, it is complete.
- A complete rainbow path uses all k colors of the coloring, whereas an incomplete rainbow path misses at least one color of the coloring.
- If a spanning subgraph of G has an (incomplete) k-rainbow coloring, then G has an (incomplete) k-rainbow coloring.
Theorem
Let G be a Hamiltonian graph of order n, where n ≥ 3. Then G has an incomplete ⌈n/2⌉-rainbow coloring, i.e, rc(G) ≤ ⌈n/2⌉.
Theorem
Let G be a 2-connected graph of order n , where n ≥ 3. Then rc(G) ≤ ⌈n/2⌉ and the upper bound is tight for n ≥ 4.
Complexity
The hardness of the rainbow connection problems has been discussed by Chakraborty et.al.
- Given an edge colored graph G, the problem of deciding if rc(G) = 2 is NP-Complete and computing rc(G) is NP-Hard.
- Given an edge-colored graph G, the problem of checking whether the given coloring makes G rainbow connected or not is NP-Complete.
- For every d > 0 there is a constant C = C(d) such that if G is a connected graph with n vertices and minimum degree at least dn, then rc(G) ≤ C. Furthermore, there is a polynomial time algorithm that constructs a corresponding coloring for a fixed d.
Now, let us consider the extension of the concept of rainbow coloring technique to the vertex coloring of graphs.
Rainbow Vertex Connected Graph
A vertex colored graph G is rainbow vertex connected if every two vertices are connected by a path whose internal vertices have distinct colors is called a rainbow vertex connected graph.Definitions
- The rainbow vertex connection number of a connected graph G denoted by rvc(G) is the smallest number of colors that are needed in order to make G rainbow vertex connected.
- A vertex colored graph G is strongly rainbow vertex connected if for every pair of distinct vertices, there exists a shortest rainbow path. Such a graph G is called a strongly rainbow vertex colored graph.
 |
| Rainbow Vertex Coloring of Tadpole Graph T3,2 |
Applications
Rainbow connection has an interesting application for secure
transfer of classified information between agencies. Hence one can find prohibitive in traders to crack the password in
sequrity information transfer. Every pair of agencies with one or more secure paths along with distinct passwords reveals the rainbow connection and is prohibitive to intruder. It is of interest to find the rc(G)
of different classes of other graphs.
References
- Chartrand, Gary.; Johns, Garry L.; McKeon, Kathleen A.; Zhang, Ping (2008), "Rainbow connection in graphs", Mathematica Bohemica 133.
- Chakraborty, Sourav; Fischer, Eldar; Matsliah, Arie; Yuster, Raphael (2011), "Hardness and algorithms for rainbow connection", Journal of Combinatorial Optimization 21 (3): 330–347.
- Faudree, R.J.; Gyarfas, A.; Lesniak, L.; Schelp, R.H. (1993). "Rainbow Coloring the Cube", Journal of Graph Theory, Vol. 17, No. 5, 607-612.
- Ramya, N.; Rangarajan, K.; Sattanathan, R. (2012). "On Rainbow Coloring of Some Classes of Graphs", International Journal of Computer Applications, Vol. 46, No. 18, 36-38.
- Arputhamary, I.A.; Mercy, H.M. (2013). "Rainbow Coloring of certain classes of graphs", International Conference on Mathematical Computer Engineering,71-78.
- Li, Xueliang.; Liu, Sujuan.; Sunil Chandran, L.; Mathew, Rogers.; Rajendraprasad, Deepak. (2012). "Rainbow Connection Number and Connectivity", The Electronic Journal of Combinatorics, Vol.19.








No comments:
Post a Comment